5 logičkih zagonetki za pronalaženje uzoraka

Umjesto upitnika, krug treba sadržavati broj 253. To je princip po kojem se formiraju brojevi u krugovima: svaki prethodni pomnoži se s 2, a rezultat se doda 3.

1 × 2 + 3 = 5.
5 × 2 + 3 = 13.
13 × 2 + 3 = 29.
29 × 2 + 3 = 61.
61 × 2 + 3 = 125.
125 × 2 + 3 = 253.

Ili je ovdje još jedan način rješavanja: svakom prethodnom broju 2 se dodaje n-tom stepenu.

1 + 2² = 1 + 4 = 5.
5 + 2³ = 5 + 8 = 13.
13 + 2⁴ = 13 + 16 = 29.
29 + 2⁵ = 29 + 32 = 61.
61 + 2⁶ = 61 + 64 = 125.
125 + 2⁷ = 125 + 128 = 253.

Umjesto upitnika, na polju treba biti slovo "P". Zbroj brojeva u svakom kvadratu redni je broj slova u abecedi. Provjerimo:

6 + 4 + 4 = 14. "M" je četrnaesto slovo u abecedi. Ubrajamo i "Yo"!
4 + 1 + 7 = 12. "K" je dvanaesto slovo u abecedi.
5 + 6 + 10 = 21. "U" je dvadeset prvo slovo u abecedi.
1 + 14 + 2 = 17. "P" je sedamnaesto slovo u abecedi, koje bi trebalo biti umjesto upitnika.

Umjesto upitnika trebao bi biti broj 179. Ako se pomičete u smjeru kazaljke na satu počevši od 3, tada je svaki sljedeći broj jednak dvostrukom prethodnom, kojem su dodani 1, 3, 5, 7, 9.

3 × 2 + 1 = 7.
7 × 2 + 3 = 17.
17 × 2 + 5 = 39.
39 × 2 + 7 = 85.
85 × 2 + 9 = 179.

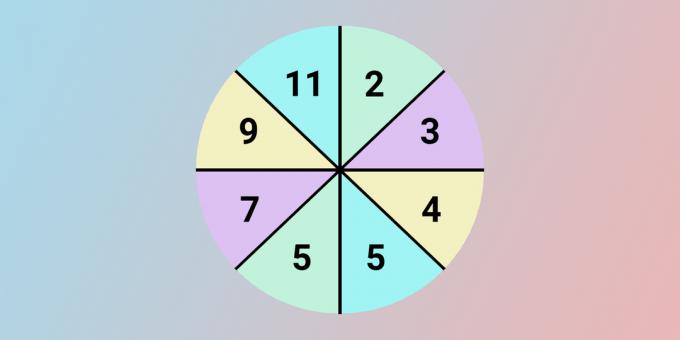
Umjesto upitnika, broj bi trebao biti 11. Da bismo dobili svaki broj s lijeve polovice kruga, uzmemo broj iz suprotnog sektora, udvostručimo i dodamo jedan.

5 = 2 × 2 + 1.
7 = 3 × 2 + 1.
9 = 4 × 2 + 1.
11 = 5 × 2 + 1.

Umjesto upitnika, broj bi trebao biti 66. Ako se pomičete u smjeru kazaljke na satu počevši od 4, svaki sljedeći broj jednak je dvostrukom prethodnom, od kojeg su oduzeta dva.

4 × 2 − 2 = 8 − 2 = 6.
6 × 2 − 2 = 12 − 2 = 10.
10 × 2 − 2 = 20 − 2 = 18.
18 × 2 − 2 = 36 − 2 = 34.
34 × 2 − 2 = 68 − 2 = 66.